向心力
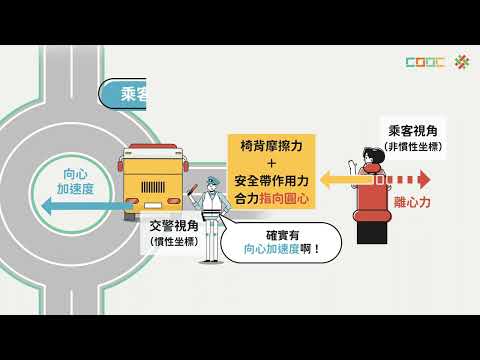
當物體沿著圓周或曲線軌跡運動時,會受到指向圓心(曲率中心)的合外力作用。這種合外力被稱為向心力。向心力可以由彈力、重力、摩擦力等任何一力產生,也可以由幾個力的合力或其分力提供。
向心力只改變所控物體的運動方向,而不改變運動的速率。非勻速圓周運動中,改變運動速率的切向加速度並非由向心力產生。

欲知向心力與線速度大小的關係,可以將角速度 ω 與線速度 v、半徑 r 聯繫起來:
$$F=m\omega^2r$$

從畢氏定理可推得:
$$d=\sqrt{r^2+D^2}-r$$
進而:
$$a=\lim_{\Delta t\to 0}\frac{2(\sqrt{r^2+D^2}-r)}{\Delta t^2}$$
若將 D 替換為 vΔt,則有:
$$a=\lim_{\Delta t\to 0}\frac{2(\sqrt{r^2+v^2\Delta t^2}}-r)}{\Delta t^2}$$
向心力是指古典力學裏當物體沿著圓周或曲線軌跡運動時,指向圓心(曲率中心)的合外力作用力。
向心力意思:深入解析維持物體旋轉的關鍵力量
向心力意思,顧名思義就是指向中心的力。它是一種作用在圓周運動物體上的力,方向永遠指向圓心的方向。向心力是維持物體在圓周運動中不會脱離軌道的重要因素,如果沒有向心力,物體將會沿直線方向運動。
向心力的概念
向心力的概念最早可以追溯到古希臘時期,亞裏士多德認為物體的運動需要持續施加推力,而當推力消失時,物體就會停止運動。直到17世紀,開普勒和伽利略的研究才改變了人們對運動的理解,他們發現即使沒有持續的推力,物體也可以保持運動,只要存在向心力。
向心力的公式
向心力的公式可以表示為:
$$F_c = m \frac{v^2}{r}$$
其中:
- $F_c$ 代表向心力
- $m$ 代表物體的質量
- $v$ 代表物體的線速度
- $r$ 代表物體運動的圓周半徑
從公式中可以看出,向心力的大小與物體的質量、線速度和圓周半徑成正比。
向心力的方向
向心力始終指向圓心的方向,這一點與其他力的方向不同。例如,重力總是指向地心,而摩擦力與物體的運動方向相反。
向心力的應用
向心力在日常生活中有很多應用,例如:
- 旋轉木馬: 當旋轉木馬旋轉時,乘客會感受到向心力,使他們不會被甩出去。
- 汽車轉彎: 當汽車轉彎時,輪胎會與地面產生摩擦力,提供向心力使汽車維持在彎道上。
- 衞星繞地球運行: 衞星繞地球旋轉時,地球的重力為其提供向心力,使它不會飛離地球。
向心力與離心力
向心力和離心力是兩個相對的概念。離心力是指物體在圓周運動中想要沿直線方向運動的力,它與向心力的大小相等,方向相反。
向心力的拓展
向心力不僅存在於圓周運動中,在任何曲線運動中都存在向心力。例如,當汽車在彎道上行駛時,輪胎與地面之間的摩擦力提供向心力,使汽車能夠沿着彎道行駛。
向心力的表格
| 特性 | 描述 |
|---|---|
| 方向 | 指向圓心 |
| 公式 | F_c = m * v^2 / r |
| 應用 | 旋轉木馬、汽車轉彎、衞星繞地球運行 |
| 拓展 | 任何曲線運動 |